Earth Cross Section for Meteoroids
For a projectile to hit a target it normally must impact within an area
which is the cross-sectional area of the target. For a spherical body, this
area is
 r2 where r
is the radius of the sphere. However, in the case of a meteoroid or an
asteroid impacting the Earth (or another planet), the appropriate
cross-sectional radius is not the physical radius of the Earth, but its
gravitational radius, which depends upon the impactor velocity.
r2 where r
is the radius of the sphere. However, in the case of a meteoroid or an
asteroid impacting the Earth (or another planet), the appropriate
cross-sectional radius is not the physical radius of the Earth, but its
gravitational radius, which depends upon the impactor velocity.
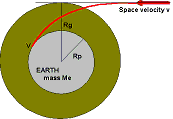
This is because the Earth's gravity will attract an impactor that might be approaching on a near miss orbit. Imagine we have an impactor that in the absence of gravity has a space velocity v, and is on a trajectory with a distance Rg from the Earth's centre. Because of gravity the trajectory will curve toward the Earth and impact with a velocity V.
This impact will be tangential if Rg is the gravitational radius of the Earth (for the space velocity v (ie the body just impacts the planet). We can use the laws of conservation of momentum aned conservation of energy to determine Rg.
v Rg = V Rp (conservation of momentum)
v2/2 = V2/2 - G Me / Rp (conservation of energy)
where G is the universal gravitational constant and Me is the mass of the Earth. Solving these two equations simultaneously we find that:
Rg = Rp √[ 2 G Me / ( v2 Rp ) + 1 ]
The table below presents values of Rg (as a function of the space velocity), both in kilometres and as a fraction of the Earth's radius. Also shown are the fractional area, and the collision velocity.
| Space vel(km/s) |
Collision vel(km/s) |
Effective radius(km) |
Fractional radius |
Fractional area |
|---|---|---|---|---|
| 2 | 11 | 36237 | 5.68 | 32.26 |
| 4 | 12 | 18942 | 2.97 | 8.81 |
| 5 | 12 | 15630 | 2.45 | 6 |
| 6 | 13 | 13494 | 2.12 | 4.47 |
| 8 | 14 | 10965 | 1.72 | 2.95 |
| 10 | 15 | 9571 | 1.5 | 2.25 |
| 15 | 19 | 7958 | 1.25 | 1.56 |
| 20 | 23 | 7309 | 1.15 | 1.31 |
| 25 | 27 | 6989 | 1.1 | 1.2 |
| 30 | 32 | 6809 | 1.07 | 1.14 |
| 35 | 37 | 6698 | 1.05 | 1.1 |
| 40 | 42 | 6625 | 1.04 | 1.08 |
| 45 | 46 | 6574 | 1.03 | 1.06 |
| 50 | 51 | 6538 | 1.02 | 1.05 |
Material prepared by John Kennewell





