Satellite Lifetimes and Solar Activity
All satellites in Earth orbit are subject to various perturbing influences which can alter their orbit. Satellites in low Earth orbit, with perigee altitudes (the lowest altitude of the orbit) below 2000 km, are subject to atmospheric drag. This force slowly circularises and reduces the altitude of the orbit. The rate of 'decay' of the orbit becomes very rapid at altitudes less than 200 km. Upon reaching an altitude of 180 km the satellite will have just a few hours left before it makes a fiery re-entry to the Earth. The temperatures attained during re-entry are usually great enough to vapourise most of the satellite, but if it is particularly large, component pieces may reach the ground.
The rate at which a low satellite orbit decays is a function of atmospheric density at each point along the orbit together with the satellite's cross sectional area and mass.
The air density varies along the orbit, being a function of latitude and longitude, time of day, time of year, and season. At a fixed point in space, the atmospheric density can be well expressed in terms of just two space environmental parameters; the solar 10 cm radio flux, denoted 10.7cm or F10, and the geomagnetic index Ap. As each of these increase we find a corresponding increase in the atmospheric density at altitudes above about 120 km.
The uncertainty associated with predicting space weather and variations in atmospheric density mean there is always an uncertainty of at least 10% in predicting when a satellite will undergo re-entry. For example, even one day before a particular re-entry is due there is an uncertainy of at least 2 hours in the predicted time of re-entry. Since a satellite can circle the globe in less than 2 hours it is obviously very difficult to predict the re-entry location.
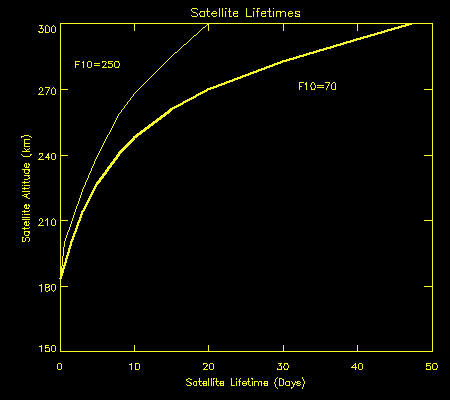
The graph below gives an indication of the lifetime of a satellite with effective mass to cross-section ratio of 100 kg/m2, in a circular orbit below 300 km. The two curves are for solar maximum (F10=250) and solar minimum (F10=70). The geomagnetic field is assumed to be quiet during this period. For mass to cross-sectional area ratio less than 100, lifetimes scale linearly. That is, for 50 kg/m2 half the lifetime, for 25 kg/m2 divide by 4 and so on.
Material prepared by John Kennewell and Andrew McDonald





