Solar Escape Velocity

On the surface of any body in space (such as a planet or star), there is a certain minimum speed that must be given to an object, which when directed vertically upwards will allow the object to escape the gravitational pull of that body, and for the Earth it has a value of 11 km/s.

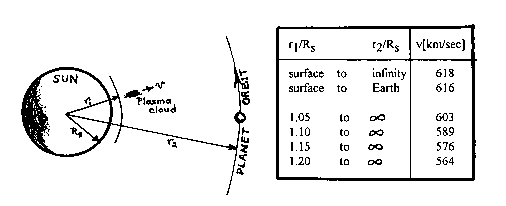
The Sun, being much more massive than the Earth, has a much larger escape velocity of around 600 km/s. Even so, activity on the Sun is often so violent that this velocity is exceeded and clouds of material are ejected into interplanetary space.

The exact speed required for solar plasma to reach a planet in the solar system depends on the distance of the planet from the Sun (r₂), and the height in the atmosphere from which the ejection takes place (r₁). This is given by the formula:

v = √ { 2 G M ( 1/r₁ - 1/r₂ ) }

where v is in units of metres per second; M is the mass of the Sun (1.991x10³⁰ kg) and G is the Universal Gravitation constant (6.67x10^-11 N(m/kg)²).

Escape velocities from various heights are given in the table below. Heights are given in terms of the radius of the Sun (denoted Rs).

When observing mass ejections from the Sun, there is a very simple rule - escape velocity has been achieved if the material moves 0.1 solar radius (70,000 km) in less than 2 minutes.

;

Material prepared by John Kennewell